Согласно ЕМ СПТ “коридор нормы определяется средним значением и стандартным отклонением”.
Но это описание границ нормы возможно только для признаков, распределение которых носит нормальный характер.
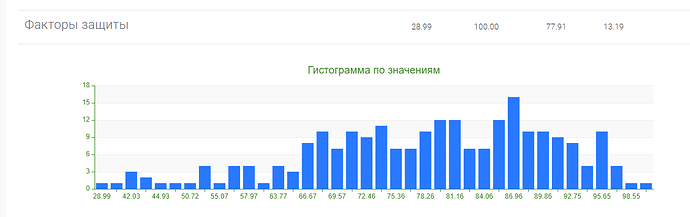
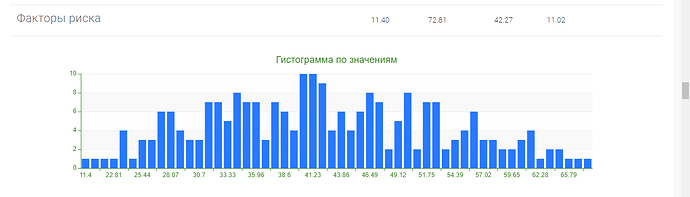
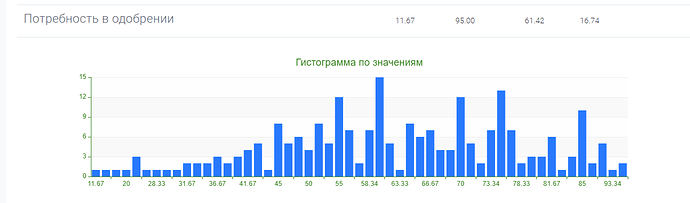
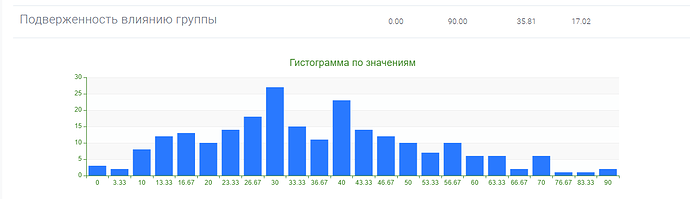
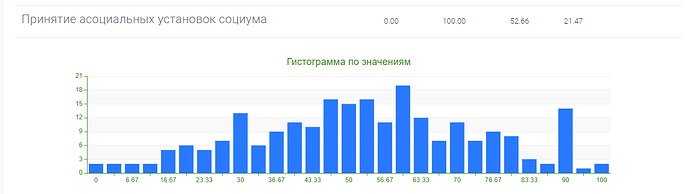
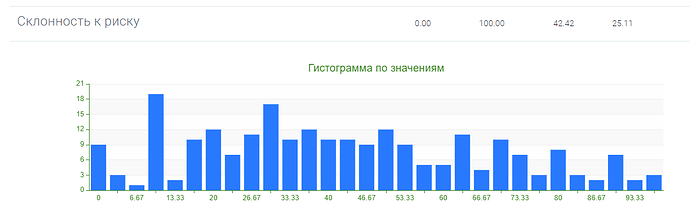
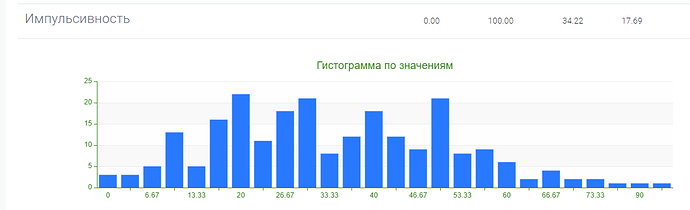
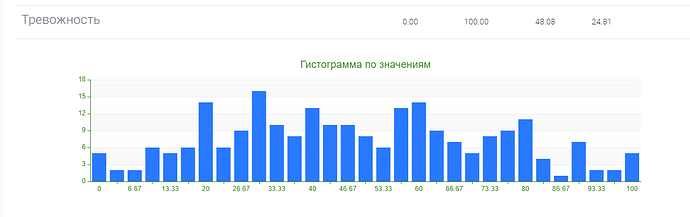
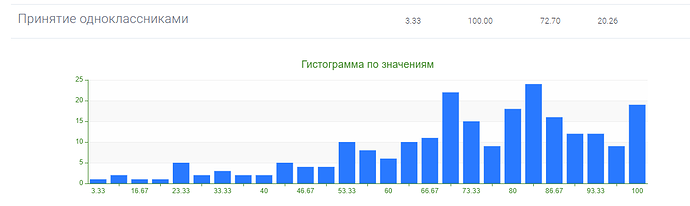
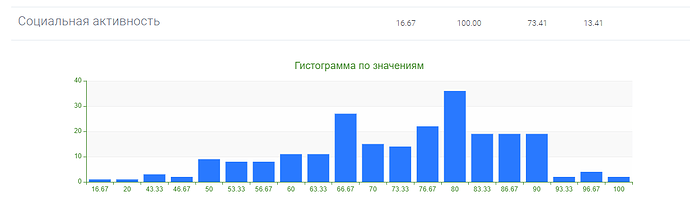
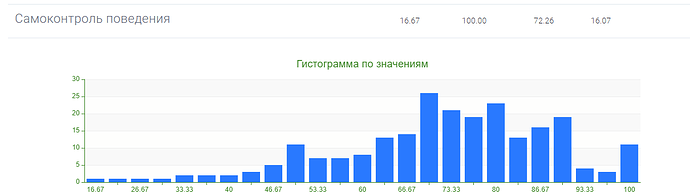
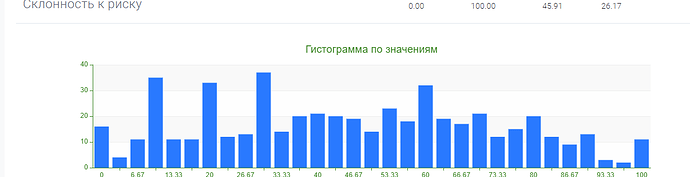
Однако после обработки результатов тестовой выборки, стало ясно, что распределения результатов по субшкалам и показателям методики квазишкалирование, не совпадают с нормальным распределением.
Это видно как на гистограммах, так и подтверждается расчетами с использованием критерия Колмогорова-Смирнова: гипотеза о том, что распределение признака является нормальным, отвергается на уровне значимости \alpha =0,05 для всех субшкал, а также для показателей “фактор риска” и “фактор защиты” методики квазишкалирование.
Для таких распределений понятия среднее и стандартное отклонение утрачивают смысл, поскольку они дают неправильное описание распределения переменной.
В медицинской, психологической, социологической статистике распределения, отличные от нормального, принято описывать при помощи медианы и интерквартильного размаха. Медиана – это значение признака, которое делит весь ряд значений пополам, то есть половина значений признака меньше медианы, и половина – больше неё. Интерквартильный размах – это интервал между 25 и 75 процентилями, то есть четверть всех значений признака будут меньше 25 процентили, а четверть – больше 75 процентили. Таким образом, интерквартильный размах содержит «центральные» 50% значений признака.
Это описание правильно характеризует реальное распределение признака.
Важно заметить, что понятие медианы и интерквартильного размаха вполне применимо и к нормальному распределению. В этом случае медиана будет равна среднему, а в пределах интерквартильного размаха будет находиться чуть меньше значений (50% всех значений), чем в пределах одного стандартного отклонения (с помощью функции Лапласа легко вычислить, что оно составляет 68% всех значений). Таким образом, коридор нормы будет определяться средним и стандартным отклонением, в соответствии с ЕМ СПТ.
Итак, если x_i - количество анкет с баллами, равными i, то нижняя граница нормы это наибольшее натуральное число Q_1, удовлетворяющее условию:
\frac{1}N\sum_{j=0}^{Q_1}{x_j}\le0,25
Верхняя граница это наименьшее натуральное число Q_2, удовлетворяющее условию:
\frac{1}N\sum_{j=0}^{Q_2}{x_j}\ge0,75
Где N - общий объем выборки (количество респондентов)
Для стандартизации вычисленные границы переводятся в проценты делением на максимально возможное количество баллов в субшкале (30 баллов).